This is an old revision of the document!
Table of Contents
Using a Wikipedia-based Semantic Relatedness Measure for Document Clustering
written by Stephen Tratz and Eduard Hovy (Information Sciences Institute, University of Southern Carolina)
presented by Martin Popel
reported by Michal Novák
Introduction
The paper describes a high-quality conversion of Penn Treebank to dependency trees. The authors introduce an improved labeled dependency scheme based on the Stanford's one. In addition, they extend the non-directional easy-first first algorithm of Goldberg and Elhadad to support non-projective trees by adding “move” actions inspired by Nivre's swap-based reordering for shift-reduce parsing. Their parser is capable of producing shallow semantic annotations for prepositions, possesives and noun compounds.
Notes
Dependency conversion structure
- in general, there are (at least) 3 possible types of dependency labels:
- unlabeled - is it really a set of labels?
- coarse labels of the CoNLL tasks
- 10-20 labels
- for example NMOD is always under a noun - it's an easy task and the result is not quite useful
- their scheme is based on the Stanford's dependency labels
Conversion process
- converting phrase trees of Penn Treebank to dependency ones
- it consists of 3 steps:
- add structure to flat NPs
- constituent-to-dependency converter with some head-finding rule modifications
- a list of rules in Figure 2 is hardly understandable without reading a paper their conversion method is related to
- they reduced the number of generic “dep/DEP” relation
- Stanford tags are hierarchical and “dep/DEP” is the top-most one
- 1.3% of arcs are non-projective (out of 8.1% of all non-projective arcs) because of the following conversion (agreement can be a motivation for this, i.e. in Czech):
Parser
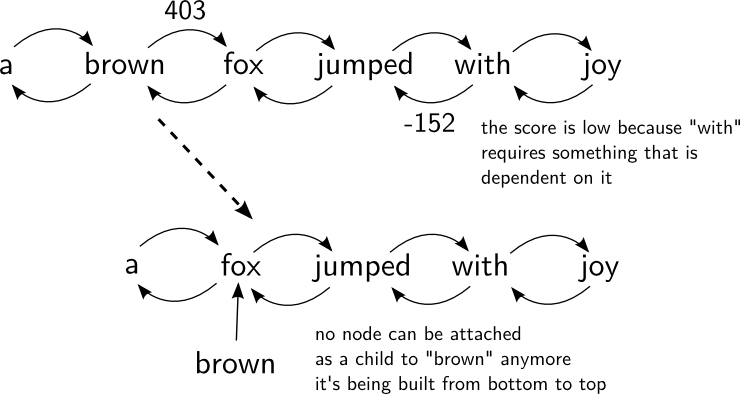
- we illustrated a step of the parser:
- we compared time complexity of this system with other commonly used ones
| MST parser | <latex>\mathop O(n | 2)</latex> | ||
|---|---|---|---|---|
| MALT parser | <latex>\mathop O(n)</latex> | in fact slower | ||
| this parser | <latex>\mathop O(n\log(n))</latex> | <latex>\mathop O(n | 2)</latex> - naive implementation | |
| this parser - non-projective | <latex>\mathop O(n | 2\log(n))</latex> | <latex>\mathop O(n | 3)</latex> - naive implementation |
- implemented by a heap, it can reach <latex>\mathop O(n\log(n))</latex>; however, they don't use it because it's fast enough
- Algorithm1
- we weren't sure what the variable “index” is (best index of parent or any index of queue of unprocessed words)
- it again confirms that pseudocode is usually more confusing than a normal code or verbal explanation